자, 아까 아빠키와 아들키에 대한 것을 잠시 봤습니다.

여기 라인을 보면 H(x) = Wx + b 와 같은 일차함수 형태로 나타낼 수 있습니다.
그런데 데이터가 많아지면서, 저런 라인을 아래와 같이 여러개를 그을 수 있겠죠?

그러면 어떤 라인을 쓰는 것이 가장 효율적인가? 라는 말이
어떤 라인을 쓰는 것이 머신러닝의 정확도가 높은가? 라는 말과 같다고 생각할 수 있습니다.
이 가설이 이 라인에서 얼마나 떨어져 있는가? 에 대한 값을 알아봅니다.
아까 봤던 저 위에 애들의 점을 확대해보겠습니다.

여기 보시면 저 점들이, 라인이랑 조금조금씩 떨어져 있습니다.
그래서 얘들이 얼마나 떨어져있는지 주황색 선으로 나타내 봤습니다.

그래서 여기서 드는 생각이, 저 주황색 선을 다 더한 값이 가장 작은 선을 구하면, 최적의 머신러닝 모델을 만들 수 있지 않을까? 라고 생각했습니다.
그러면 저 선을 식으로 나타내서 처리해줘야 하는데, 식으로 표현해보면 H(x) - y 를 다 더하면 될 것 같은데, 이렇게 그대로 하면 음수가 나올 수도 있으니, 제곱을 해 줍니다.
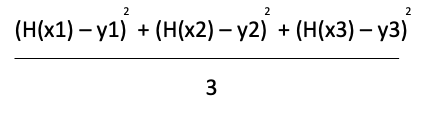
만약에 얘가 N개라면 아래와 같이 식이 나눠지게 됩니다.

자 그러면 얘를 좀 더 수학적으로 나타내봅니다.

자, 그러면 위에 보이는애가 cost함수입니다.
그럼 얘를 최소화하면 될 것 같은데, 어떻게 최소화하지? 라는 의문이 드실 수 있습니다.
그런데 쟤를 보다보면 예전에 봤던 애와 비슷하게 생겼습니다.
우리가 학교다닐 때 봤던 수학 공식과 비슷하게 생겼는데
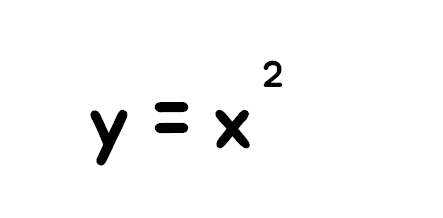
이런 애를 그래프로 그리면 아래와 같이 생겼는데

얘를 최소화하는 부분을 찾는 것 입니다.

그렇다면, 어떻게 해야할까... 하고 보니, 경사도가 가장 작은 구간을 찾으면 됩니다.
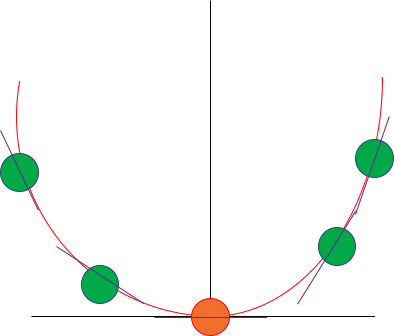
이 경사도가 가장 작은 부분을 찾는 방법을 경사하강법(gradient descent algorithm) 이라고 합니다.
참조
[1] - https://www.youtube.com/watch?v=Hax03rCn3UI
'유튜브 > 대충 배우는 머신러닝 AI(영상삭제)' 카테고리의 다른 글
| 8 - regression 실습2 (0) | 2020.01.31 |
|---|---|
| 7 - regression 실습 (0) | 2020.01.31 |
| 5 - 회귀(linear regression) (0) | 2020.01.31 |
| 4 - 주피터 노트북 (0) | 2020.01.31 |
| 3 - 텐서플로, 파이토치, 사이킷런, 케라스 (0) | 2020.01.28 |